Third Scientific Lecture-Course:
Astronomy
GA 323
Lecture IX
9 January 1921, Stuttgart
We have now reached a point in our studies from which we must proceed with extreme caution, in order to see where there is a danger of allowing our thought to depart from reality and to see also when we are avoiding this danger, by keeping within the bounds of what is real.
Last time, we suggested the comparison of two facts: The appearance within the planetary system of the cometary phenomena, and, alas within the planetary system, though perhaps not bearing quite the same relationship to it, all that we observe in the phenomena of fertilization. In order, however, to come to ideas about this which are at all justified, we must first see whether it is indeed possible to find connections between two so widely separated things, with which we are confronted in the external world of facts. In scientific method, we shall not make real progress, unless we can refer from one realm of facts to another, manifesting something of a similar nature and thus leading us on.
We have seen how on the one hand we have to use the element of figure and form, the mathematical, and then how we are again and again impelled to come to terms in one way or another with the qualitative aspect, in some way to find a qualitative approach. And so today we will bring in something which arises in regard to man if one really studies this man, who is, after all, in some way an image of the heavenly phenomena,—as the many statements in these lectures may enable us to deduce. Yet we still have to establish in what way he is this image. If this is what he is, we must first of all gain a clear understanding of man himself. We must understand the picture from which we intend to take our start,—understand its inner perspective. Just as in looking at a painting one must know what a foreshortening means, and so on, in order to pass from the picture to the real spatial relationships and to relate the picture to what it represents in reality, so, if we would approach reality in the universe, interpreting it through man, we must first be clear about man. Now it is, extraordinarily difficult, as a human being, to come near to the human being with palpable ideas. Therefore, I should like today to bring before your souls what I might call “palpably impalpable” thought-pictures arising from quite simple foundations, ideas with which most of you are probably already well acquainted, but which we must nevertheless bring before our minds in a certain connection. These ideas, which seem in part to be quite easy to grasp and yet again, beyond certain limits, to elude our comprehension, will afford us a means of orientation in the striving to take hold of the outer world through ideas.
It may appear somewhat forced to keep emphasizing the necessity of referring back to man's life of pictorial imagination in order to understand the phenomena of the heavens. But after all it is obvious that however carefully we may describe the heavenly phenomena, we have, to begin with, nothing more than a form of optical picture, permeated with mathematical thoughts. What Astronomy gives us has fundamentally the character of a picture. To be on the right path, we must therefore concern ourselves with the arising of the picture in man, otherwise we shall gain no true relationship to what Astronomy can say to us. And so I should like today to proceed from some quite simple mathematics and to show you how, in a different domain from that to which we were led through the ratios of the periods of revolution of the planets, there appears within Mathematics itself this element of the incomprehensible, the impalpable. We meet with it when in a certain connection we study quite familiar curves. (As I said, many of you already know what I am about to describe, I only want to elucidate the subject today from a particular aspect.)
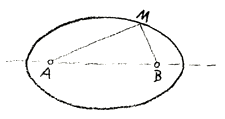
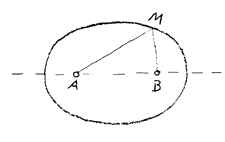
Consider the Ellipse, with its two foci \(A\) and \(B\), and you know that it is a definition of the ellipse that for any point \(M\) of the curve, the sum of its distances \((a + b)\) from the two foci remains constant. It is characteristic of the ellipse, that the sum of the distances of any one of its points from two fixed points, the two foci, remains constant (Fig. 1).
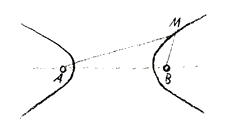
Then we have a second curve, the Hyperbola (Fig. 2). You know that it has two branches. It is defined in that the difference of the distances of any point of the curve from the two foci, \((b - a)\) is a constant magnitude. In the ellipse, then, we have the curve of the constant sum, in the hyperbola, the curve of constant difference, and we must now ask: What is the curve of constant product?
I have often drawn attention to this: The curve of constant product is the so-called Curve of Cassini (Fig. 3). We find it when, having two points, \(A\) and \(B\), we consider a point M in regard to its distances from \(A\) and \(B\), and establish the condition that the two distances \(AM\) and \(BM\) multiplied together should equal a constant magnitude. For the sake of simplicity in the calculation, I will call the constant magnitude \(b^2\) and the distance \(AB\), \(2a\). If we take the mid-point between \(a\) and \(b\) as the center of the axes of a co-ordinate system and calculate the ordinates for each point that fulfills these conditions,—take \(C\) as the center of the co-ordinate system and let the point whose ordinate we will call y move round so that for each point of the curve \(AM•BM = b^2\), we get the following equation. (I will only give you the result, for the simply reason that everyone can easily work out the calculation for himself; it is to be found in any mathematical text-book relating to the subject.) We find for \(y\) the value:
$$y=±\sqrt{-(a^2+x^2)±\sqrt{b^4+4a^2x^2}}$$Taking here into account that we cannot use the negative sign because we should then have an imaginary y, and considering therefore taking only the positive sign, we have:
If we then draw the corresponding curve, we have a curve, rather like but not identical with an ellipse, called the curve of Cassini (Fig. 4). It is symmetrical to the left and right of the ordinate axis and about and below the abscissa axis.

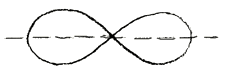
But now, this curve has various forms, and for us at any rate this is the important thing about it. The curve has different forms, according to whether b, as I have taken it here, is greater than a, equal to a, or less than a. The curve I have just drawn arises when b ˃ a, and furthermore when another condition is fulfilled, namely, that b is also greater than or equal to a √2. Moreover, when b ˃ a√2, there is a distinct curvature above and below, If b = a√2, then at this point above and below, the line of the curve becomes straightened,m it flattens so much that it almost becomes a straight line (Fig. 4). If, however, b ˂ a√2, then the whole course of the curve is changed and it takes on this form (Fig. 5). And if b = a, the curve passes over into a quite special form, it changes into this form (Fig. 6). It runs back into itself, cuts through itself and comes out on the other side, and we obtain the special form of the Lemniscate. The lemniscate, then, is a special form of Curve of Cassini—these curves are so named after their discoverer. The particular form assumed by the curve is determined by the ratio between the constant magnitudes which appear in the equation characterizing the curve. In the equation, we have only these two constant magnitudes, b and a, and the form of the curve depends on the ratio between them.

Then the third case is possible, that b ˂ a. If b ˂ a, we can still find values for the curve. We can always solve the equation and obtain values for the curve, ordinates and abscissae, even when b is smaller than a, only the curve then undergoes yet another metamorphosis. For when b ˂ a, we find two branches of the curve, which look something like this (Fig. 7). We have a discontinuous curve. And here we come to the point where the mathematics itself confronts us with what I called the “palpably impalpable”, something that is difficult to grasp in space. For in the sense of the mathematical equation, this is not two curves, but one; it is a single curve in exactly the same way as all these are single curves (Figs. 3 through 5). In this one (the lemniscate) there is already a transition. The point which describes the curve takes this path, goes round underneath, cuts its previous path here and continues on here (Fig. 7). Here, we must picture the following: If we let the point M move along this line, it does not simply cross over from one side to the other,—it does not do this. It runs along the path just as in the other curves, describes a curve here, but then manages to turn up again here (Fig. 7) You see, that which carries the point along the line disappears here in the middle. If you want to understand the curve you can only imagine that it disappears in the middle. If you try to form a continuous mental picture of this curve, what must you do?
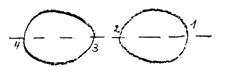
It is quite easy, is it not, to imagine curves such as thes. (I only say this in parenthesis for the ordinary philistine!) You can go on imagining points along the curve and you do not find that the picture breaks off. Here (in the lemniscate) admittedly, you have to modify the comfortable way of simply going round and round, but still it goes on continuously. You can keep hold of the mental picture. But now, when you come to this curve (Fig. 7), which is not so commonplace, and you want to image it, then, in order to keep the continuity of the idea you will have to say: Space no longer gives me a point of support. In crossing over to the other branch in my imagination, unless I break the continuity and regard the one branch as independent of the other, I must go out of space; I cannot remain in space. So you see, Mathematics itself provides us with facts which oblige us to go out of space, if we would preserve the continuity of the idea. The reality itself demands of us that in our ideas we go out of space. Even in Mathematics therefore we are confronted with something which shows us that in some way we must leave space behind, if the pure idea is to follow its right path. Having ourselves and going the idea is beginning to think the process through, we must go on thinking in such a way that space is no longer of any help to us. If this were not so, we should not be able to calculate all possibilities in the equation.
In pursuing similar line of thought, we meet with other instances of this kind. I will only draw your attention to the next step, which ensures if one things as follows. The ellipse is the locus of the constant sum,—it is defined by the fact that is is the curve of constant sum. The hyperbola is the curve of constant difference. The curve of Cassini in its various forms is the curve of constant product. There must then be a curve of constant quotient also, if we have here A, here B, here a point M, and then a constant quotient to be formed through the division of BM by AM. We must be able to find different points, M 1, M 2, etc., for which
$$\frac{BM_1}{AM_1}=\frac{BM_2}{AM_2}$$etc. are equal to one another and always equal to a constant number. This curve is, in fact, the Circle. If we look for the points M1, M2 etc. we find a circle which has this particular relationship to thee points A and B (Fig. 8). So that we can say: Besides the usual, simple definition of a circle,—namely, that it is the locus of a point whose distance from a fixed point remains constant,—there is another definition. The circle is that curve, very point of which fulfills the condition that its distances from two fixed points maintain a constant quotient.
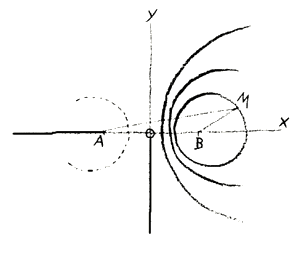
Now, in considering the circle in this way there is something else to be observed. For you see, if we express this
$$\frac{BM}{AM}=\frac{m}{n}$$(it could of course be expressed in some other way), we always obtain corresponding values in the equation, and we can find the circle. In doing this we find different forms of the circle (that is, different proportions between the radius of the circle and the length of the straight line AB), according to the proportion of m to n. These different forms of the circle behave in such a way that their curvature becomes less and less. When \(n\) is much greater than m, we find a circle with a very strong curvature; when n is not so much greater, the curvature is less. The circle becomes larger and larger the smaller the difference between n and m. And if we follow this proportion of m to n still further, the circle gradually passes over into a straight line. You can follow this in the equation. It passes over into the ordinate axis itself. The circle becomes the ordinate axis when \(m=n\), that is, when the quotient \(m/n=1\). In this way the circle gradually changes into the ordinate axis, into a straight line.
You need not be particularly astonished at this. It is quite possible to imagine. But something very different happens it we wish to follow the process still further. The circle has flattened more and more, and through becoming flatter from within, as it were, it changes into a straight line. It does this because the constant ratio in the equation undergoes a change. Through this the circle becomes a straight line. But this constant ratio can of course grow beyond \(1\), so that the arcs of the circles appear here (on the left of the \(y\)-axis). What must we do, however, if we try to follow it in our imagination? We have to do something quite peculiar. We have, in fact, to think of a circle which is not curved towards the inside, but is curved towards the outside. Of course, I cannot draw this circle, but it is possible to think of a circle which is curved towards the outside.1If it were drawn it would look like an ordinary circle, only one would have to bear in mind that “outside” and “inside” had changed places. (Editor's note.) In an ordinary circle the curvature is towards the inside, it is not? If we follow the line round it returns into itself. But defining the circle in this other way, if we use the necessary constant, we obtain a straight line. The curvature is still on this side (right of the \(y\)-axis). But it now makes things not nearly so comfortable for us as before! Previously, the curvature always turned towards the center of the circle, while now (in the case of the straight line), we are shown that the center is somewhere in the infinite distance, as one says. Following on from this, there arises for us the idea of a circle which is curved towards the outside. Its curvature is then no longer as it is here (Fig. 9a)—that would be the ordinary, commonplace, philistine circle,—but its curvature is here (Fig. 9b). Therefore, the inside of this circle is not here; this is the outside; the inside of this circle (Fig. 9c) is to the right.
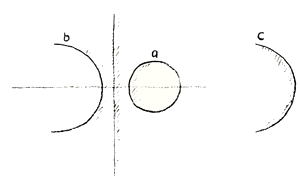
Now compare what I have just put before you. I have described the curve of Cassini, with its various forms, the lemniscate and the form in which there are two branches. And now we have pictured the circle in such a way that at one time it is curved in the familiar way, with the inside here and the outside here; while in a second form of circle (in drawing it we are only indicating what is meant) we find that the curvature is this way round, with an inside here and an outside here. Comparing it with the Cassini curve, the first form of the circle would correspond to the closed forms, as far as the lemniscate. After this we have another kind of circle, which must be thought of in the other direction, being curved this way, with the inside here and the outside here. You see, when we are concerned with the constant product we find forms of the curve of Cassini where, it is true, we are thrown out of space, yet we can still draw the other branch on the other side. The other branch is once more in space, although in order to pass from the one to the other we are thrown out of space. Here, in the case of the circle, however, the matter becomes still more difficult. In the transition from circle to straight line we are, indeed, thrown out of space, and moreover, we can no longer draw a self-contained form at all. This we are unable to do. In passing over from the curve of constant product to the curve of constant quotient, we are only just able to indicate the thought spatially.
It is extraordinarily important that we concern ourselves with the creating of ideas which, as it were, will still slip into such curve-forms. I am convinced that most people who concern themselves with mathematics take note of such discontinuities, but then make the thought more comfortable by simply holding to the formula and not passing on to what should accompany the mathematical formula in true continuity of thought. I have also never seen that in the treatment of Mathematics as subject matter for education any great value is laid upon the forming of such thoughts in imagination.—I do not know,—I ask the mathematicians present, Herr Blümel, Herr Baravalle, if this is so; whether in modern University education any importance is attached to this? (Dr. Unger here mentioned the use of the cinema.) Yes, but that is a pretense. It is only possible to represent such things within empirical space by means of the cinema or in similar ways, it some sort of deception is introduced. It cannot be pictured fully in real space without the effect being achieved through some form of deception. The point is, whether there is anywhere in the sphere of reality something which obliges us to think realistically in terms of such curves. This is the question I am now asking. Before passing on, however, to describe what might perhaps correspond to these things in the realm of reality, I should like to add something which may perhaps make it easier for you to pass transition from these abstract ideas to the reality. It is the following.
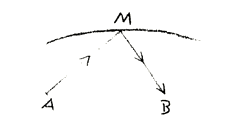
You can set another problem in the sphere of theoretical Astronomy, theoretical Physics. You can say: Let us suppose that here as \(A\), is a source of light, and this source of light in a illumines a point \(M\) (Fig. 10). The strength of the light shining from \(M\) is observed from \(B\). That is, with the necessary optical instruments, observation is made from \(B\) of the strength of the light shining from the point \(M\), which is illumined from \(A\). And of course, the strength of the light would vary, according to the distance between \(B\) and \(M\). But there is a path which could be described by the point \(M\), such that, being illumined from A, it always shines back to \(B\) with the same intensity. There is such a path; and we can therefore ask: What must be the locus of a point, illumined from a fixed point \(A\), such that, seen from another fixed point \(B\), its light is always of the same intensity? This curve—the curve in which such a point would have to move—is the curve of Cassini! From this you see that something which takes on a qualitative nature is set into spatial connection, fitting into a complicated curve. The quality that we must see in the beam of light—for the intensity of light is a quality—depends in this case on the element of form in the spatial relationships.
I only wished to bring this forward for you to see that there is at least some way of leading over from what can be grasped in geometrical form to what is qualitative. This way is a long one, and what we will now discuss is something to which I want to draw your attention, although it would take months to present in all detail. You must be fully aware that I only intend to give you guiding lines; it is left to you to develop them further and to go into all the details which would testify to the truth of what is said. For you see, the connection which must be formed between spiritual science and empirical sciences of today demands very far-reaching and extensive work. But when lines of direction are once given, this work can to some extent be undertaken and carried forward. It is at all events possible. One must only be able in a quite definite way to penetrate into the empirical phenomena.
If we now tackle the problem from quite another angle,—we have sought to some degree to understand it from the mathematical aspect, then, to anyone who is studying the human organism, there is something which cannot escape unnoticed, something which has often been brought forward in our circle, especially in the talks which accompanied the course of lectures on Medicine in Dornach in the spring of 1920. It is not to be overlooked that certain relationships exist between the organisation of the head and the rest of the human organisation, for example the metabolism. There is indeed a connection, indefinable to begin with, between what takes place in the third system of the human being—in all the organs of metabolism—and what takes place in the head. The relationship is there, but it is hard to formulate. Clearly as it emerges in various phenomena,—for example, it is obvious that certain illnesses are connected with skull or head deformities and the like, and these things can easily be traced by one who tries to follow them with biological reasoning,—it nevertheless difficult to grasp this relationship in imagination. People do not usually get beyond the point of saying that there must be some sort of connection between what takes place in the head, for instance, and in the rest of the human organism. It is a picture which is difficult to form, just because it is so very hard for people to make the transition from the quantitative aspect to the qualitative. If we are not educated through spiritual-scientific methods to find this transition, quite independently of what outer experience offers,—to extend to what is qualitative the kind of thought we use for what is quantitative, if we do not methodically train ourselves to do this, then, my dear friends, there will always be an apparent limit to our understanding of the external phenomena.
Let me indicate but one way in which you can train yourselves methodologically to think the qualitative in a similar way as you think the quantitative. You are all acquainted with the phenomenon of the solar spectrum, the usual continuous spectrum. You know that we have there the transition of colour from red to violet. You know, too, that Goethe wrestled with the problem of how this spectrum is in a sense the reverse of what must arise if darkness be allowed to pass through the prism in the same way as is usually done with light. The result is a kind of inverted spectrum, and as you know Goethe arranged this experiment also. In the ordinary spectrum, the green passes over on the one side towards the violet and on the other towards the red; whereas in the spectrum obtained by Goethe in applying a strip of darkness to the prism there is peach-blossom in the middle and then again red on the one side and violet on the other (Fig. 11). The two colour bands are obtained, the centres of which are opposite to one another, qualitatively opposite, and both bands seem to stretch away as it were into infinity. But now, one can imagine that this axis, the longitudinal axis of the ordinary spectrum, is not simply a straight line, but a circle, as indeed every straight line is a circle. If this straight line is a circle, it returns into itself, and we can consider the point where the peach-blossom appears to be the same point as the one in which the violet, stretching to the right, meets the red, which stretches to the left. They meet in the infinite distance to the right and left. If we were to succeed—maybe you know that one of the first experiments to be made in our newly established physical laboratory is to be in this direction—if we were to succeed in bending the spectrum in a certain way into itself, then even those who are not willing to grasp the matter to begin with in pure thought will be able to see that we are here concerned with something real and of a qualitative nature.

We come to certain limiting ideas in Mathematics, where—as in Synthetic Geometry—we are obliged to regard the straight line as a circle in a quite real though inner sense; where we are obliged to admit of the infinitely distant point of a straight line as being only one point; or to understand as bounding a plane, not some line above and then again below, but a single straight line; or to think of the boundary of infinite space, not in the nature of something spherical, but as a plane. Such ideas, however, also become, in a way, limiting ideas for sense-perceptible empirical reality, and we are made to realise it if we insist on restricting ourselves to sense-perceptible reality.
This brings us to something which would otherwise always remain perpetually in the dark. I have already mentioned it. It invites us really to think-through the thought-pictures to which we come when we allow the lemniscate-form of the Cassini curve to pass over into the double-branched form,—the form with the two branches for which we must go out of space,—and them compare this with what confronts us in the empirical reality.
You are indeed already doing this, my dear friends, when you apply Mathematics in one way or another to the empirical reality. You call a triangle a triangle, because you have first constructed it mathematically. You apply to the outer form what has been evolved in an inner constructive way within you. The process I have just described is only more complicated, but it is the same process when you think of the two branches of that particular form of the Cassini curve as one. Apply this thought to the correspondence between the human head and the rest of the human organism and you will have to realise that in the head there is a connection with the remaining organism of precisely such a character as is expressed by the equation which requires, not a continuous curve, but a discontinuous one. This cannot be followed anatomically; you must go out beyond what the body comprises physically, if you would find the connection of what comes to expression in the head with what comes to expression in the metabolic system. It is essential to approach the human organism with thoughts which are quite unattainable if for every element of the thought you insist on an entire correspondence within the sense-perceptible empirical realm. We must reach out to something else, beyond the sense-perceptible empirical realm, if we are to find what this relationship really is within the human being.
Such a study, if one really gives oneself up to it and carried it out methodically, is extraordinarily rich in its results. The human organisation is of such a nature that it cannot be embraced by the anatomical approach alone. Just as we are driven out of space in the Cassini curve, so in the study of man we are driven out of the body, by the method of study itself. You see, it is quite possible to understand in the first place in thought, that in a study of the whole man we are driven out of the realm of what can be grasped in a physical-empirical sense. To put forward such things is no offence against scientific principles. Such ideas are far removed from the purely hypothetical fantasies which are often entertained in connection with natural phenomena, for they refer to the whole way in which man is membered into the universe. You are not looking for something which is otherwise non-existent, but rather for something which is exactly the same as what is expressed in the relationship between a man thinking mathematically and the empirical reality.
It is not a question of looking for hypotheses which in the end are unjustifiable; it is a question, since the reality is obviously complicated, of looking for other cognitive relations to the inner reality, in addition to the simple relation of mathematical man to empirical reality. When once you have accepted such thoughts, you will also be led to ask whether what takes place outside the human being in other domains besides the astronomical,—for example, in those phenomena which we call the chemical and physical,—whether those same phenomena, which we regard as chemical phenomena outside of man, take the same course within man, when he is alive, as they do outside him, or whether here, too, a transition is necessary which leads in some way out of space.
Now consider the important question arising out of this. Suppose we have here some kind of chemical phenomena and here the boundary leading over to the inside of the human being (Fig. 13). Supposing that this chemical phenomenon were able to call forth another, so that the human being reacted here (inside); then, if we remain in the field of the empirical, space would of course be the mediator. If, however, the continuance of this phenomenon within the human being comes about by virtue of the fact, say, that the human being is nourished by food, and the processes already taking place outside him continue inside him, then the question arises: Does the force which is at work in the chemical process remain in the same space when it taking place within man as when it is taking its course outside him? Or must we perhaps go out of space?
And there you have what is analogous to the circle which changes over into a straight line. If you look for its other form, where what is usually turned outward is now turned inward, you are entirely outside of space.
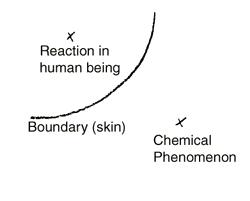
The question is, whether we do not need such ideas as these, thought-pictures which, while remaining continuous, go right out of space,—when we follow the course of what happens outwardly, outside of man, into the interior of the human being. The only thing to be said against such things, my dear friends, is that they certainly impose greater demands on the human capacity of understanding than the ideas with which he phenomena are approached today. They might therefore be rather awkward in University education. They are, no doubt, thoroughly awkward, for they imply that before approaching the phenomena we must awaken in ourselves what will enable us to understand them. Nothing like this exists in our educational system today; but it must come, it must certainly come, otherwise simply in speaking of a phenomenon we get into the greatest disparities, without in any way seeing the reality. Just think what happens when someone observes the circle as it curves to this side (Fig. 9a), and then sees how it curves to this side (Fig. 9b), but then remains a philistine and simple does not conceive that the circle now curves towards the other side. He says: This is impossible, the circle cannot curve this way; I must put the curvature this way round, I must simply place myself on the other side. What he is speaking about seems to be one and the same thing; but he has changed his point of view.
In this way today we make matters simple, in describing what is within the human being in comparison with what takes place in Nature outside him. We say: What is within man does not exist at all; I must simply place myself within man and say that the curvature is facing this way (Fig. 9c). I will then consider what is inside, without taking into account that I have reversed the curvature. I will make the interior of the human being into an outer Nature. I simply imagine outer Nature to continue through the skin into the interior. I turn myself round, because I am not willing to admit the other form of curvature, and then I theorise. That is the trick which is performed today, only in order to adhere to more comfortable motions. There is no desire to accent what is real; in order not to have to do so, we simply turn ourselves round, and—this is now a comparison—instead of looking at the human from in front, we look at Nature from behind and thus arrive in this way at all the various theories concerning man.
We will continue, then, tomorrow.

