Education
GA 307
IX. Arithmetic, Geometry, History
Ilkley, 14th August, 1923
Arithmetic and geometry, indeed all mathematics, occupy a unique position in education. Education can only be filled with the necessary vitality and give rise to a real interplay between the soul of the teacher and the soul of the child, if the teacher fully realizes the consequences of his actions and methods. He must know exactly what effect is made on the child by the treatment he receives in school, or anywhere else.
Man is a being of body, soul and spirit; his bodily nature is formed and moulded by the spirit. The teacher, then, must always be aware of what is taking place in the soul and spirit when any change occurs in the body, and again, what effect is produced in the body when influences are brought to bear on the life of spirit or soul.
Anything that works upon the child's conceptual and imaginative faculties, anything that is to say of the nature of painting or drawing which is then led over into writing, or again, botany taught in the way indicated yesterday, all this has a definite effect. And here, above all, we must consider a higher member of man's being, a member to which I have already referred as the etheric body, or body of formative forces. The human being has, in the first place, his physical body. It is revealed to ordinary physical sense-perception. Besides this physical body, however, he has an inner organization, perceptible only to Imaginative Cognition, a super-sensible, etheric body. Again he has an organization perceptible only to Inspiration, the next stage of super-sensible knowledge. (These expressions need not confuse us; they are merely terms.) Inspiration gives insight into the so-called astral body and into the real Ego, the Self of the human being.
From birth till death, this etheric body, this body of formative forces which is the first super-sensible member of man's being never separates from the physical body. Only at death does this occur. During sleep, the etheric organization remains with the physical body lying there in bed. When man sleeps, the astral body and Ego-organization leave the physical and etheric bodies and enter them again at the moment of waking.
Now it is the physical and etheric bodies which are affected when the child is taught arithmetic or geometry, or when we lead him on to writing from the basis of drawing and painting. All this remains in the etheric body and its vibrations persist during sleep. On the other hand, history and such a study of the animal kingdom as I spoke of in yesterday's lecture work only upon the astral body and Ego-organization. What results from these studies passes out of the physical and etheric bodies into the spiritual world during sleep.
If, therefore, we are teaching the child plant-lore or writing, the effects are preserved by the physical and etheric bodies during sleep, whereas the results of history lessons or lessons on the nature of man are different, for they are carried out into the spiritual world by the Ego and astral body. This points to an essential difference between the effects produced by the different lessons.
We must realize that all impressions of an imaginative or pictorial nature made on the child have the tendency to become more and more perfect during sleep. On the other hand, everything we tell the child on the subject of history or the being of man works on his organization of soul and spirit and tends to be forgotten, to fade away and grow dim during sleep. In teaching therefore, we have necessarily to consider whether the subject-matter works upon the etheric and physical bodies or upon the astral body and Ego-organization.
Thus on the one hand, the study of the plant kingdom, the rudiments of writing and reading of which I spoke yesterday affect the physical and etheric bodies. (I shall speak about the teaching of history later on.) On the other hand, all that is learnt of man's relation to the animal kingdom affects the astral body and Ego-organization, those higher members which pass out of the physical and etheric bodies during sleep. But the remarkable thing is that arithmetic and geometry work upon both the physical-etheric and the astral and Ego. As regards their role in education arithmetic and geometry are really like a chameleon; by their very nature they are allied to every part of man's being. Whereas lessons on the plant and animal kingdoms should be given at a definite age, arithmetic and geometry must be taught throughout the whole period of childhood, though naturally in a form suited to the changing characteristics of the different life-periods.
It is all-important to remember that the body of formative forces, the etheric body, begins to function independently when it is abandoned by the Ego and astral body. By virtue of its own inherent forces, it has ever the tendency to bring to perfection and develop what has been brought to it. So far as our astral body and Ego are concerned, we are—stupid, shall I say? For instead of perfecting what has been conveyed to these members of our being, we make it less perfect. During sleep, however, our body of formative forces continues to calculate, continues all that it has received as arithmetic and the like. We ourselves are then no longer within the physical and etheric bodies; but supersensibly, they continue to calculate or to draw geometrical figures and perfect them. If we are aware of this fact and plan our teaching accordingly, great vitality can be generated in the being of the child. We must, however, make it possible for the body of formative forces to perfect and develop what it has previously received.
In geometry, therefore, we must not take as our starting point the abstractions and intellectual formulae that are usually considered the right groundwork. We must begin with inner, not outer perception, by stimulating in the child a strong sense of symmetry for instance.
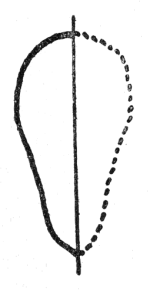
Even in the case of the very youngest children we can begin to do this. For example: we draw some figure on the blackboard and indicate the beginning of the symmetrical line. Then we try to make the child realize that the figure is not complete; he himself must find out how to complete it. In this way we awaken an inner, active urge in the child to complete something as yet unfinished. This helps him to express an absolutely right conception of something that is a reality. The teacher, of course, must have inventive talent but that is always a very good thing. Above all else the teacher must have mobile, inventive thought.
When he has given these exercises for a certain time, he will proceed to others. For instance, he may draw some such figure as this (left) on the blackboard, and then he tries to awaken in the child an inner conception of its spatial proportions. The outer line is then varied and the child gradually learns to draw an inner form corresponding to the outer (right). In the one the curves are absolutely straightforward and simple. In the other, the lines curve outwards at various points. Then we should explain to the child that for the sake of inner symmetry

he must make in the inner figure an inward curve at the place where the lines curve outwards in the outer figure. In the first diagram a simple line corresponds to another simple line, whereas in the second, an inward curve corresponds to an outward curve.

Or again we draw something of this kind, where the figures together form a harmonious whole. We vary this by leaving the forms incomplete, so that the lines flow away from each other to infinity. It is as if the lines were running away and one would like to go with them. This leads to the idea that they should be bent inwards to regulate and complete the figure, and so on. I can only indicate the principle of the thing. Briefly, by working in this way, we give the child an idea of “a-symmetrical symmetries” and so prepare the body of formative forces in his waking life that during sleep it elaborates and perfects what has been absorbed during the day. Then the child will wake in an etheric body, and a physical body also, inwardly and organically vibrant. He will be full of life and vitality. This can, of course, only be achieved when the teacher has some knowledge of the working of the etheric body; if there is no such knowledge, all efforts in this direction will be mechanical and superficial.
A true teacher is not only concerned with the waking life but also with what takes place during sleep. In this connection it is important to understand certain things that happen to us all now and again. For instance, we may have pondered over some problem in the evening without finding a solution. In the morning we have solved the problem. Why? Because the etheric body, the body of formative forces, has continued its independent activity during the night.
In many respects waking life is not a perfecting but a disturbing process. It is necessary for us to leave our physical and etheric bodies to themselves for a time and not limit them by the activity of the astral body and Ego. This is proved by many things in life; for instance by the example already given of someone who is puzzling over a problem in the evening. When he wakes up in the morning he may feel slightly restless but suddenly finds that the solution has come to him unconsciously during the night. These things are not fables; they actually happen and have been proved as conclusively as many another experiment. What has happened in this particular case? The work of the etheric body has continued through the night and the human being has been asleep the whole time. You will say: “Yes, but that is not a normal occurrence, one cannot work on such a principle.” Be that as it may, it is possible to assist the continued activity of the etheric body during sleep, if, instead of beginning geometry with triangles and the like, where the intellectual element is already in evidence, we begin by conveying a concrete conception of space. In arithmetic, too, we must proceed in the same way. I will speak of this next.
A pamphlet on physics and mathematics written by Dr. von Baravalle (a teacher at the Waldorf School) will give you an excellent idea of how to bring concreteness into arithmetic and geometry. This whole mode of thought is extended in the pamphlet to the realm of physics as well, though it deals chiefly with higher mathematics. If we penetrate to its underlying essence, it is a splendid guide for teaching mathematics in a way that corresponds to the organic needs of the child's being. A starting-point has indeed been found for a reform in the method of teaching mathematics and physics from earliest childhood up to the highest stages of instruction. And we can apply to the domain of arithmetic what is said in this pamphlet about concrete conceptions of space.
Now the point is that everything conveyed in an external way to the child by arithmetic or even by counting deadens something in the human organism. To start from the single thing and add to it piece by piece is simply to deaden the organism of man. But if we first awaken a conception of the whole, starting from the whole and then proceeding to its parts, the organism is vitalised. This must be borne in mind even when the child is learning to count. As a rule we learn to count by being made to observe purely external things—things of material, physical life.
First we have the 1—we call this Unity. Then 2, 3, 4, and so forth, are added, unit by unit, and we have no idea whatever why the one follows the other, nor of what happens in the end. We are taught to count by being shown an arbitrary juxtaposition of units. I am well aware that there are many different methods of teaching children to count, but very little attention is paid nowadays to the principle of starting from the whole and then proceeding to the parts. Unity it is which first of all must be grasped as the whole and by the child as well. Anything whatever can be this Unity. Here we are obliged to illustrate it in a drawing. We must therefore draw a line; but we could use an apple just as well to show what I shall now show with a line.
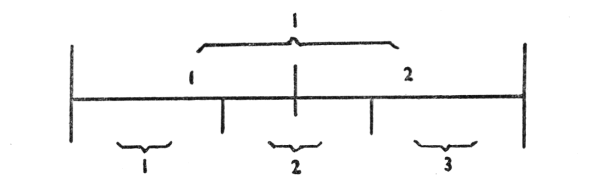
This then is 1. And now we go on from the whole to the parts, or members. Here then we have made of the 1 a 2, but the 1 still remains. The unit has been divided into two. Thus we arrive at the 2. And now we go on. By a further partition the 3 comes into being, but the unit always remains as the all-embracing whole. Then we go on through the 4, 5, and so on. Moreover, at the same time and by other means we can give an idea of the extent to which it is possible to hold together in the mind the things that relate to number and we shall discover how really limited man is in his power of mental presentation where number is concerned.
In certain nations to-day the concept of number that is clearly held in the mind's eye only goes up to 10. Here in this country money is reckoned up to 12. But that really represents the maximum of what is mentally visualised for in reality we then begin over again and in fact count what has been counted. We first count up to 10, then we begin counting the tens, 2 times 10=20, 3 times 10=30. Here we are no longer considering the things themselves. We begin to calculate by using number itself, whereas the more elementary concept requires the things themselves to be clearly present in the mind.
We are very proud of the fact that we are far advanced in our methods of counting compared with primitive peoples who depend on their ten fingers. But there is little foundation for this pride. We count up to 10 because we sense our hands as members. We feel our two hands symmetrically with their 10 fingers. This feeling also arises and is inwardly experienced by the child, and we must call forth the sense of number by a transition from the whole to the parts. Then we shall easily find the other transition which leads us to the counting in which one is added to another. Eventually, of course, we can pass on to the ordinary 1, 2, 3, etc. But this mere adding of one or more units must only be introduced as a second stage, for it has significance only here in physical space, whereas to divide a unity into its members has an inner significance such that it can continue to vibrate in the etheric body even though quite beneath our consciousness. It is important to know these things.
Having taught the child to count in this way, the following will also be important. We must not pass on to addition in a lifeless, mechanical way merely adding one item to another in series. Life comes into the thing when we take our start not from the parts of the addition sum but from the sum total itself. We take a number of objects; for example, a number of little balls. We have now got far enough in counting to be able to say: Here are 14 balls. Now we divide them, extending this concept of a part still further. Here we have 5, here 4, here 5 again. Thus we have separated the sum into 5 and 4 and 5. That is, we go from the sum to the items composing it, from the whole to the parts. The method we should use with the child is first to set down the sum before him and then let the child himself perceive how the given sum can be divided into several items.
This is exceedingly important. Just as to drive a horse we do not harness him tail foremost, so in the teaching of arithmetic we must have the right direction. We must start from a whole which is always actually present, from a reality, from what is present as a whole and then pass on to the separate parts; later, we find our way to the ordinary addition sum.
Continuing thus, from the living whole to the separate parts, one touches the reality underlying all arithmetical calculations: i.e., the setting in vibration of the body of formative forces. This body needs a living stimulus for its formative activity and once energised it will continually perfect the vibrations without the need of drawing upon the astral body and Ego-organization with their disturbing elements.
Your teaching work will also be essentially enhanced and vivified if you similarly reverse the other simple forms of calculation. To-day, one might say, they are standing on their heads and must be reversed. Try, for instance, to bring the child to say: “If I have 7, how much must I take away to get 3,” instead of “What remains over if I take 4 from 7?” That we have 7 is the real thing and that 3 remains is also real; how much must we take away from 7 to get 3? Beginning with this form of thought we stand in the midst of life, whereas with the opposite form we are dealing with abstractions. Proceeding in this way, we can easily find our way further. Thus, once more, in multiplication and division we should not ask what will result when we divide 10 into two parts, but how must we divide 10 to get the number 5. The real aspect is given; moreover in life we want eventually to get at something which has real significance. Here are two children, 10 apples are to be divided among them. Each of them is to get 5. These are the realities. What we have to deal with is the abstract part that comes in the middle. Done in this way, things are always immediately adapted to life and should we succeed in this, the result will be that what is the usual, purely external way of adding, by counting up one thing after another with a deadening effect upon the arithmetic lessons, will become a vivifying force, of especial importance in this branch of our educational work. And it is evident that precisely by this method we take into account the sub-conscious in man, that is, the part which works on during sleep and which also works subconsciously during the waking hours. For one is aware of a small part only of the soul's experience; nevertheless the rest is continually active. Let us make it possible for the physical and etheric bodies of the child to work in a healthy way, realizing that we can only do so if we bring an intense life, an awakened interest and attention, especially into our teaching of arithmetic and geometry.
The question has arisen during this Conference as to whether it is really a good thing to continue the different lessons for certain periods of time as we do in the Waldorf School. Now a right division of the lessons into periods is fruitful in the very highest degree. “Period” teaching means that one lesson shall not perpetually encroach upon another. Instead of having timetables setting forth definite hours:—8 – 9, arithmetic, 9 – 10, history, religion, or whatever it may be, we give one main lesson on the same subject for two hours every morning for a period of three, four, or five weeks. Then for perhaps five or six weeks we pass on to another subject, but one which in my view should develop out of the other, and which is always the same during the two hours. The child thus concentrates upon a definite subject for some weeks.
The question was asked whether too much would not be forgotten, whether in this way the children would not lose what they had been taught. If the lessons have been rightly given, however, the previous subject will go on working in the subconscious regions while another is being taken. In “period” lessons we must always reckon with the subconscious processes in the child. There is nothing more fruitful than to allow the results of the teaching given during a period of three or four weeks to rest within the soul and so work on in the human being without interference.
It will soon be apparent that when a subject has been rightly taught and the time comes round for taking it up again for a further period it emerges in a different form from what it does when it has not been well taught. To make the objection that because the subjects will be forgotten it cannot be right to teach in this way, is to ignore the factors that are at work. We must naturally reckon on being able to forget, for just think of all we should have to carry about in our heads if we could not forget and then remember again! The part played by the fact of forgetting therefore as well as the actual instruction must be reckoned with in true education.
This does not mean that it should be a matter for rejoicing whenever children forget. That may safely be left to them! Everything depends on what has so passed down into the subconscious regions, that it can be duly recalled. The unconscious belongs to the being of man as well as the conscious. In regard to all these matters we must realize that it is the task of education to appeal not only to the whole human being, but also to his different parts and members. Here again it is essential to start from the whole; there must first be comprehension of the whole and then of the parts. But to this end it is also necessary to take one's start from the whole. First we must grasp the whole and then the parts. If in counting we simply place one thing beside another, and add, and add, and add, we are leaving out the human being as a whole. But we do appeal to the whole human being when we lay hold of Unity and go from that to Numbers, when we lay hold of the sum, the minuend, the product and thence pass on to the parts.
The teaching of history is very open to the danger of our losing sight of the human being. We have seen that in really fruitful education everything must be given its right place. The plants must be studied in their connection with the earth and the different animal species in their connection with man. Whatever the subject-matter, the concrete human element must be retained; everything must be related in some way to man.
But when we begin to teach the child history, we must understand that at the age when it is quite possible for him to realize the connection of plant-life with the earth and the earth itself as an organism, when he can see in the human being a living synthesis of the whole animal kingdom, he is still unable to form any idea of so-called causal connections in history. We may teach history very skilfully in the ordinary sense, describing one epoch after another and showing how the first is the cause of the second; we may describe how in the history of art, Michelangelo followed Leonardo da Vinci, for instance, in a natural sequence of cause and effect. But before the age of twelve, the child has no understanding for the working of cause and effect, a principle which has become conventional in more advanced studies. To deduce the later from the earlier seems to him like so much unmusical strumming on a piano, and it is only by dint of coercion that he will take it in at all. It has the same effect on his soul as a piece of stone that is swallowed and passes into the stomach. Just as we would never dream of giving the stomach a stone instead of bread, so we must make sure that we nourish the soul not with stones but with food that it can assimilate. And so history too, must be brought into connection with Man and to that end our first care must be to awaken a conception of the historical sequence of time in connection with the human being.
Let us take three history books, the first dealing with antiquity, the second with the Middle Ages, and the third with our modern age. As a rule, little attention is paid to the conception of time in itself. But suppose I begin by saying to the child: “You are now ten years old, so you were alive in the year 1913. Your father is much older than you and he was alive in the year 1890; his father, again, was alive in 1850. Now imagine that you are standing here and stretching your arm back to someone who represents your father; he stretches his arm back to his father (your grandfather), now you have reached the year 1850.” The child then begins to realize that approximately one century is represented by three or four generations. The line of generations running backwards from the twentieth century brings him finally to his very early ancestors. Thus the sixtieth generation back leads into the epoch of the birth of Christ. In a large room it will be possible to arrange some sixty children standing in a line, stretching an arm backwards to each other. Space is, as it were, changed into time.
If the teacher has a fertile, inventive mind, he can find other ways and means of expressing the same thing—I am merely indicating a principle. In this way the child begins to realize that he himself is part of history; figures like Alfred the Great, Cromwell and others are made to appear as if they themselves were ancestors. The whole of history thus becomes an actual part of life at school when it is presented to the child in the form of a living conception of time.
History must never be separated from the human being. The child must not think of it as so much book-lore. Many people seem to think that history is something contained in books, although of course it is not always quite as bad as that. At all events, we must try by every possible means to awaken a realization that history is a living process and that man himself stands within its stream.
When a true conception of time has been awakened, we can begin to imbue history with inner life and soul, just as we did in the case of arithmetic and geometry, by unfolding not a dead but a living perception. There is a great deal of quibbling to-day about the nature of perception, but the whole point is that we must unfold living and not dead perception. In the symmetry-exercises of which I spoke, the soul actually lives in the act of perception. That is living perception. Just as our aim is to awaken a living perception of space, so must all healthy teaching of history given to a child between the ages of nine and twelve be filled with an element proceeding in this case not from the qualities of space, but from the qualities of heart and soul.
The history lessons must be permeated through and through with a quality proceeding from the heart. And so we must present it as far as possible in the form of pictures. Figures, real forms must stand there and they must never be described in a cold, prosaic way. Without falling into the error of using them as examples for moral or religious admonition, our descriptions must nevertheless be coloured with both morality and religion. History must above all lay hold of the child's life of feeling and will. He must be able to enter into a personal relationship with historic figures and with the modes of life prevailing in the various historical epochs. Nor need we confine ourselves merely to descriptions of human beings. We may, for instance, describe the life of some town in the twelfth century, but everything we say must enter the domains of feeling and will in the child. He must himself be able to live in the events, to form his own sympathies and antipathies. His life of feeling and will must be stimulated.
This will show you that the element of art must everywhere enter into the teaching of history. The element of art comes into play when, as I often describe it, a true economy is exercised in teaching. This economy can be exercised if the teacher has thoroughly mastered his subject-matter before he goes into the classroom; if it is no longer necessary for him to ponder over anything because if rightly prepared it is there plastically before his soul. He must be so well prepared that the only thing still to be done is the artistic moulding of his lesson. The problem of teaching is thus not merely a question of the pupil's interest and diligence, but first and foremost of the teacher's interest, diligence and sincerity.
No lesson should be given that has not previously been a matter of deep experience on the part of the teacher. Obviously, therefore, the organization of the body of teachers must be such that every teacher is given ample time to make himself completely master of the lessons he has to give.
It is a dreadful thing to see a teacher walking round the desks with a book in his hands, still wrestling with the subject-matter. Those who do not realize how contrary such a thing is to all true principles of education do not know what is going on unconsciously in the souls of the children, nor do they realize the terrible effect of this unconscious experience. If we give history lessons in school from note-books, the child comes to a certain definite conclusion, not consciously, but unconsciously. It is an unconscious, intellectual conclusion, but it is deeply rooted in his organism: “Why should I learn all these things? The teacher himself doesn't know them, for he has to read from notes. I can do that too, later on, so there is no need for me to learn them first.” The child does not of course come to this conclusion consciously, but as a matter of fact when judgments are rooted in the unconscious life of heart and mind, they have all the greater force. The lessons must pulsate with inner vitality and freshness proceeding from the teacher's own being. When he is describing historical figures for instance the teacher should not first of all have to verify dates. I have already spoken of the way in which we should convey a conception of time by a picture of successive generations. Another element too must pervade the teaching of history. It must flow forth from the teacher himself. Nothing must be abstract; the teacher himself as a human being must be the vital factor.
It has been said many times that education should work upon the being of man as a whole and not merely on one part of his nature. Important as it is to consider what the child ought to learn and whether we are primarily concerned with his intellect or his will, the question of the teacher's influence is equally important. Since it is a matter of educating the whole nature and being of man, the teacher must himself be “man” in the full sense of the word, that is to say, not one who teaches and works on the basis of mechanical memory or mechanical knowledge, but who teaches out of his own being, his full manhood. That is the essential thing.

