Third Scientific Lecture-Course:
Astronomy
GA 323
Lecture IV
4 January 1921, Stuttgart
If I had the task of presenting my subject purely according to the methods of Spiritual Science, I should naturally have to start from different premises and we should be able to reach our goal more quickly. Such a presentation, however, would not fulfill the special purpose of these lectures. For the whole point of these lectures is to throw a bridge across to the customary methods of scientific thought. Admittedly, I have chosen just the material which makes the bridge most difficult to construct, because the customary mode of thought in this realm is very far from realistic. But in contending against an unreal point of view, it will become apparent how we can emerge from the unsatisfying nature of modern theories and came to a true grasp of the facts in question. Today, then, I should like to consider the whole way in which ideas have been formed in modern times about the celestial phenomena.
We must, however, distinguish two things in the formation of these ideas. First, the ideas1Note by translators: In the first few pages of this lecture, the word Vorstellungen has been translated, either as “mental pictures” or “thought-pictures”, or by the word “ideas” as in Prof. Hoernle's original English edition of Dr. Steiner's Philosophie der Freiheit. In other translations, including the later editions of this book, the word is rendered “representations”, or again, “Mental presentations”. Dr. Steiner's use of Vorstellung corresponds, we believe, to the colloquial, work-a-day meaning of the word “idea” in current English. (Where Idea is meant in its deeper, more spiritual meaning—German Idee—it can be distinguished by the use of a capital.) are derived from observation of the celestial phenomena, and theoretical explanations are then linked on to the observations. Sometimes very far-reaching, spun-out theories have been linked on to relatively few observations. That is the one thing, namely, that a start is made from observations out of which certain ideas have been developed. The other is that, the ideas having been reached, they are further elaborated into hypotheses. In this creating of hypotheses,—a process which ends in the setting up of some definite cosmology,—much arbitrariness prevails, since in the setting-up of theories, any preconceived ideas existing in the minds of those who put forward the theory, make themselves strongly felt.
I will therefore first call your attention to something which will perhaps strike you as paradoxical, but which, when carefully examined, will none the less prove fruitful in the further course of our studies.
In the whole mode of thought of modern Science there prevails what might be called, and indeed has been called, the ‘Regula philosophandi’. It consists in saying: What has been traced to definite causes in one realm of reality, is to be traced to the same causes in other realms. In setting up such a ‘regula philosophandi’ the starting-point is as a rule apparently self-evident. It will be said—scientists of the Newtonian school will certainly say—that breathing must have the same causes in man as in the animal, or again, that the ignition of a piece of wood must have the same cause whether in Europe or in America. Up to this point the thing is obvious enough. But then a jump is made which passes unnoticed,—is taken tacitly for granted. Those who are wont to think in this way will say, for example, that if a candle and the Sun are both of them shedding light the same causes must surely underlie the light of the candle and the light of the Sun. Or again, if a stone falls to Earth and the Moon circles round the Earth, the same causes must underlie the movement of the stone and the movement of the Moon. to such an explanation they attach the further thought that if this were not so, we should have no explanations at all in Astronomy. The explanations are based on earthly things. If the same causality did not obtain in the Heavens as on Earth, we should not be able to arrive at any theory at all.
Yet when you come to think of it, this regula philosophandi is none other than a preconceived idea. Who in the world will guarantee that the causes of the shining of a candle and of the shining of the Sun are one and the same? Or that in the falling of a stone, or the falling of the famous apple from the tree by which Newton arrived at his theory, there is the same underlying cause as in the movements of the heavenly bodies? This would first have to be established. As it is, it is a mere preconceived idea. Prejudices of this kind enter in, when, having first derived theoretical explanations and thought—pictures inductively from the observed phenomena, people rush headlong into deductive reasoning and construct world-systems by deductive methods.
What I am now describing thus abstractly has, however, become a historical fact. There is a continuous line of development from what the great thinkers at the opening of the modern age—Copernicus, Kepler, Galileo—concluded from comparatively few observations. Of Kepler—notably of his third Law, quoted yesterday—it must be said that his analysis of the facts which were available to him is a work of genius.
It was a very great intensity of spiritual force which Kepler brought to bear when, from the little that lay before him, he discovered this ‘law’ as we call it, or better, this ‘conceptual synthesis’ of the phenomena of the universe. Then however, by way of Newton a development set in which was not derived from observation but from theoretical constructions, including concepts of force and mass and the like, which we must simply omit if we only want to hold to what is given. The development in this direction reaches a culminating point—conceived, admittedly, with genius and originality—in Laplace, where it leads to a genetic explanation of the entire cosmic system (as you will convince yourselves if you read his famous book Exposition du Systeme du Monde ), or again in Kant, in his Natural History and Theory of the Heavens. In all that has followed in this trend we see the effort constantly made to come to conclusions based on the thought pictures that have thus been conceived of the connections of the celestial movements, and resulting in such explanations of the origin of the universe as the nebular theory and so on.
It must be noted that in the historical development of these theories we have something which is put together from inductions made, once again, with no little genius in this domain—and from subsequent deductions in which the special predilections of their authors were included. Inasmuch as a thinker was imbued with materialism it was quite natural for him to mingle materialistic ideas with his deductive concepts. Then it was no longer the facts which spoke, for one proceeded on the basis of the theories which had emerged from the deductions. Thus, for example, inductively men first arrived at the mental pictures which they summed up in the notion of a central body, the Sun, with the planets revolving around it in ellipses according to a certain law, namely: the radius-vectors describe equal areas in equal periods of time. By observing the different planets of a solar system, it was moreover possible to summarize their mutual relations in Kepler's third law: ‘For different planets the squares of the periods of revolution are proportional to the cubes of the radius-vectors’. Here was a certain picture. The question, however, was not decided, whether this picture completely fitted the reality. It was in truth an abstraction from reality; to what extent it related to the full reality, was not established. From this picture—not from reality, but from this picture—people deduced what then became a whole genetic system of Astronomy. All this must be borne in mind. Modern man is taught from childhood as if the theories which have been reached in the past few centuries by deductive reasoning were the real facts. We will therefore, while taking our start from what is truly scientific, disregard as far as is possible all that is merely theoretical and link on to those ideas which only depart from reality to the extent that we shall still be able to discover in them a connection with what is real. It will be my task, in all that I give to-day, to follow the direction of modern scientific thought only up to those ideas and concepts which still permit one to find the way back again into reality. I shall not depart so far from reality that the concepts become crude enough to allow of the deduction of nebular hypotheses.
Proceeding in this way,—pursuing the modern method of forming concepts in this particular field,—we must first form a concept which presented itself inductively to Kepler and was then developed further I repeat expressly, I will only go so far in these concepts that even if the picture in the form in which it was conceived should be mistaken, it has departed only so far from reality that it will be possible to eliminate the mistake and return to what is true. We need to develop a certain flair for reality in the concepts we entertain. We cannot proceed in any other way if we wish to throw a bridge across from the reality to the spun-out theories of modern scholarship and science.
Here then, to begin with, is a concept which we must examine. The planets have eccentric orbits,—they describe ellipses. This is something with which we can begin. The planets have eccentric orbits and describe ellipses, in one focus of which is the Sun. They describe the ellipses in accordance with the law that the radius—vectors describe equal areas in equal periods of time.
A second essential for us to hold to is the idea that each planet has its own orbital plane. Although the planets carry out their evolutions in the neighborhood of each other, so to speak, yet for each planet there is the distinct plane of its orbit, more or less inclined to the plane of the Sun's equator: If this depicts the plane of the Sun's equator (Fig.1), an orbital plane of a planet would be thus; it would not coincide at all with the plane of the Sun's equator.2Note by Editor: This plane is inclined at an angle of about seven degrees to the plane of the ecliptic.
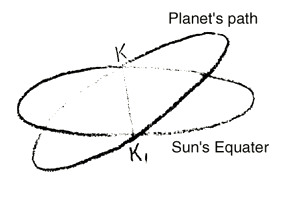
These are two very significant mental pictures, to be formed from the facts of observation. And yet, in the very forming of them we must take note of something in the real world-picture, which as it were, rebels against them. For instance, if we are trying to understand our solar system in its totality, and only base it upon the picture of the planets moving in eccentric orbits, the orbital planes being inclined at varying degrees to the plane of the solar equator, we shall be in difficulties if we also take into account the movements of the comets. The moment we turn our attention to the cometary movements, the picture no longer suffices. The outcome will be better understood from the historical facts than from any theoretical explanations.
Upon these two thought-pictures,—that the orbital planes of the planets lie in the proximity of the plane of the Sun's equator, and that the orbits are eccentric ellipses,—Kant, Laplace and their successors built up the nebular hypothesis. Follow what emerges from this. At a pinch, and indeed only at a pinch, it is a way of imagining the origin of the solar system. But the astronomical system thus constructed contains no satisfactory explanation of the part played by the cometary bodies. They always fall out of the theory. This discordance of the comets with the theories which were formed, as described, in the course of scientific history, proves that the cometary life somehow rebels against a concept formed, not from the whole but only from a part of the whole. We must be clear, too, that the paths of the comets frequently coincide with those of other bodies which also play into our system and present a riddle precisely through their association with the comets. These are the meteoric swarms, whose paths very frequently—perhaps even always—coincide with the cometary paths. Here, my dear friends, taking into account the totality of our system, we are led to say: A sea of ideas has gradually been formed from the study of our planetary system as a whole,—ideas with which we cannot do justice to the seemingly irregular and almost arbitrary paths of the comets and meteoric swarms. They simply refuse to be included in the more abstract pictures that have been reached. I should have to give you long historical descriptions to show in detail how many difficulties have arisen in connection with the concrete facts, when the investigators—or rather, thinkers—approached the comets and meteoric swarms with their astronomical theories.
I wish only to point out the directions in which a sound understanding can be sought. We shall come to such an understanding if we pay attention to yet another aspect.
Starting in this way from concepts which still have a remnant of reality in them, we will now try to go back a little towards what is real. It is indeed always necessary to do this in relation to the outer world, in order that our concepts may not stray too far from reality,—for this is a strong propensity of man. We must go back again and again to the reality.
There is already no little danger in forming such a concept as that the planets move in ellipses, and then beginning at once to build a theory upon this concept. It is far better, after forming such a concept, to turn back to reality in order to see if the concept does not need correcting, or at least modifying. This is important. It is very clearly seen in astronomical thinking. Also in biological and especially in medical thought, the same failing has led people very far astray. They do not take into account, how necessary it is directly they have formed a concept, to go back to reality in order to make sure that there is no reason to modify it.
The planets, then, move in ellipses. But these ellipses vary; they are sometimes more circular, sometimes more elliptical. We find this if we return to reality with the ellipse idea. In the course of time the ellipse becomes more bulging, more like a circle, and then again more like an ellipse. So I by no means include the whole reality if I merely say, ‘the planets move in ellipses’. I must modify the concept and say: The planets move in paths which continually struggle against becoming a circle or remaining one and the same ellipse. If I were now to draw the elliptic line, to be true to the reality I should have to make it of india-rubber, or form it flexibly in some way, continually altering it within itself. For if I had formed the ellipse which is there in one revolution of the planet, it would not do for the next revolution, and still less for the following one. It is not true that when I pass from reality to the rigid concept I still remain within the real. That is the one thing.
The other is: We have said that the planes of the planetary orbits are inclined to the plane of the Sun's equator. Where the planets cross the point of intersection of their orbits (with the Ecliptic) in an upward or downward direction, they are said to form Nodes. The lines, joining the two Nodes (K-K 1 in Fig. 1), are variable. So too are the inclinations of the planes to one-another, so that even these inclinations, if we try to express them in a single concept, bring us to a rigid concept which we must immediately modify in face of the reality. For if an orbit is inclined at one time in one way, and at another time in another way, the concept we deduce in the first instance must afterwards be modified. To be sure, once such a point has been reached, we can take an easy line and say that there are ‘disturbances’ and that the reality is only grasped ‘approximately’ with our concepts. We then go on swimming comfortably in further theories. But in the end we swim so far that the fanciful and theoretic pictures we are constructing no longer correspond to the reality, though they are meant to do so.
It is easy to agree that this mutability of the eccentric orbits, and of the mutual inclination of the planes of the orbits, must somehow or other be connected with the life of the whole planetary system, or shall we say, with its continuing activity. It must be connected in some way with the living activity of the whole planetary system. That is quite evident. Starting from this, one might again try to form the concept, saying: Well now, I will bring such mobility into my thoughts that I picture the ellipses continually bulging out and contracting, the planes of the orbits ascending, descending and rotating, and then from this starting-point I will build up a world-system according to reality. Good. But if you think the idea through to the end, then precisely as the outcome of such logical thought, the result is a planetary system which cannot possibly go on existing. Through the summation of the disturbances which arise especially through the variability of the Nodes, the planetary system would move towards its own ultimate death and rigidity. Here there comes in what philosophers have pointed out again and again. While such a system can be thought out, in reality it would have had ample time to reach the ultimate finale. There is no reason why it should not. The infinite possibility would have been fulfilled; rigidity would long ago have set in.
We enter here into a realm where thought apparently comes to a standstill. Precisely by following my thinking through to the very last, I arrive at a world-system which is still and rigid. But that is not reality.
Now, however, we come to something else, to which we must pay special attention. In pursuing these things further—you can find the theory of it in the work of Laplace; I will only relate the phenomena—one finds that the reason why the system has not actually reached rigidity under the influence of the disturbances—the variability of the Nodes, etc.,—is that the ratios of the periods of revolution of the planets are not commensurable. They are incommensurable quantities, numbers with decimals to an infinite number of places. Thus we must say: If we compare the periods of revolution of the planets in the sense of Kepler's Third Law, the ratios of these periods cannot be given in integers, nor in finite fractions, but only in incommensurable numbers. Modern Astronomy is clear on this. It is to the incommensurability of the ratios between the periods of revolution of the several planets (in Kepler's third Law) that the planetary system owes its continued mobility. Otherwise, it must long ago have come to a standstill.
Observe now, what has happened. In the last resort, we are obliged to base our thoughts about the planetary system upon numbers which in the end elude our grasp. This is of no little importance.
We are therefore led, by the very requirements of scientific development, to think of the planetary system mathematically in such a way that the mathematical results are no longer commensurable. We are at the place, where in the mathematical process itself we arrive at incommensurable numbers. We have to let the number stand,—we come to a stop. We can write it in decimals no doubt, but only up to a certain place. Somewhere or other we must leave off when we come to the incommensurable. The mathematicians among you will be clear about this. You will see that in dealing with incommensurable number I reach the point where I must say: I calculate up to here and then I can go no further. I can only say (forgive my using a somewhat amusing comparison for a serious subject) that this coming to an inevitable halt in mathematics reminds me of a scene in which I was once a participator in Berlin. A fashion in Variety-entertainment came about through certain persons, one of whom was Peter Hill. He had founded a kind of Cabaret and wanted to read his own poems there. He was a very lovable person, in heart and soul a Theosophist, he had rather gone to seed in Bohemian circles. I went to a performance in which he read his own poems. The poem had got so far that single lines were finished, and so he read it aloud:
The Sun came up. ... etc. (The first line.)
The Moon rose. ... etc. (That was the second line.)
At each line he said ‘etc.’ That was a reading I once attended. As a matter of fact it was most stimulating. Everyone could finish the line as he chose! Admittedly with incommensurable numbers [you] cannot do this, yet here too you can only indicate the further process. You can say that the process continues in a certain direction, but nothing is given by which you might form an idea as to what numbers may yet be coming. It is important that precisely in the astronomical field we are led into incommensurabilities. We are forced by Astronomy to the very limits of mathematising; here the reality escapes us. Reality escapes us, we can say nothing else; reality eludes our grasp.
What does this mean? It means that we apply the most secure of our sciences, Mathematics, to the celestial phenomena, and in the last resort the celestial phenomena do not submit; the moment comes where they elude us. Precisely where we are about to reach their very life, they slip away into the incommensurable realm. Here then, our grasp of reality comes to an end at a certain point and passes over into chaos.
We cannot say without more ado, what this reality, which we are trying to follow mathematically, actually does when it slides away into the incommensurable. Undoubtedly this is related to its power of continued life. To enter the full astronomical reality we must take leave of what we are able to master mathematically. The calculation plainly shows this; the very history of science shows it.
Such are the points which we must work towards, if we would proceed in a realistic spirit. Now I would like to set before you the other pole of the matter. If you follow it physiologically you can begin from any point you like in embryonic development, whether it be from the development of the human embryo in the third or second month,—or the embryo of some other creature. You can follow the development back as far as ever you can with the means of modern science. (it is in fact only possible to a limited extent, as those of you who have studied it will know.) You can trace it back to a certain point, from which you cannot get much further, namely to the detachment of the ovum—the fertilized ovum. Picture to yourselves how far you can go back. If you wished to go still further back you would be entering the indeterminate realm of the whole maternal organism. This means that in going back you come into a kind of chaos. You cannot avoid this, and the fact that it cannot be avoided is shown by the course of scientific development. Think of such scientific hypotheses as the theory of “Panspermia” for instance, where they speculated as to whether the single germ-cell was prepared out of the forces of the whole organism, which was more the point of view of Darwin, or whether it developed in a more segregated way in the purely sexual organs. You will see when you study the course of scientific development in this field that no little fantasy was brought to bear on the attempt to explain the underlying genesis, when tracing backward the arising of the germ cell from the maternal organism. You come into a completely indeterminate realm. There is little but speculation in the external science of today as to the connection between the germ-cell and the maternal organism.
Then at a certain point in its development this germ appears in a very definite way, in a form which can be grasped at least approximately by mathematical or at any rate geometrical means. Diagrams can be made from a certain point onward. Many such diagrams exist in Embryology. The development of the germ-cell and other cells can be delineated more or less exactly. So one begins to picture the development in a geometrical way, representing it in forms similar to purely geometrical figures. Here we are following up a reality which in a way is the reverse of what we had in Astronomy. There we pursued a reality with our cognitional process and came to incommensurable numbers; the whole thing slips into chaos through the process of knowledge itself. In Embryology we slip out of chaos. From a certain moment onward we can grasp what emerges from chaos through forms that are like purely geometrical forms. Thus in effect, in employing Mathematics in Astronomy we come at one point into chaos. And by pure observation in Embryology we have at a certain point nothing before us but chaos; it all seems chaotic at first, observation is impossible. Then we come out of chaos into the realm of Geometry. It is therefore an ideal of certain biologists—a very justifiable ideal—to grasp in a geometrical form what presents itself in Embryology; not merely to make illustrations of the growing embryo naturalistically, but to construct the forms according to some inherent law, similar to the laws underlying geometrical figures. It is a justifiable ideal.
Now therefore we can say: When in Embryology we try to follow up the real process by observation, we emerge out of a sphere which lies about as near to our understanding as that which is beyond the incommensurable numbers. In Astronomy on the one hand, we proceed with our understanding up to the point where we can no longer follow mathematically. In Embryology on the other hand our understanding begins at a certain point, where we are first able to set to work with something resembling Geometry.
Think the thought through to its conclusion. You can do so, since it is a purely ‘methodological’ thought, that is to say the reality of it is in our own inner life.
If in arithmetic we reach the incommensurable numbers,—that is, we reach a point where the reality is no longer represented by a number that can be shown in its complete form—then we should also begin to ask whether the same thing may not happen with geometrical form as with arithmetical analysis. (We shall speak more of this in the next lecture.) The analytical process leads to incommensurable number. Now let us ask: How do geometrical forms image the celestial movements? Do not these images perhaps lead us to a certain point. Similar to that to which arithmetical analysis is leading when we reach incommensurable number? Do we not in our study of the heavenly bodies—namely the planets—come to a boundary, at which we must admit we can no longer use geometrical forms as a means of illustration; the facts can no longer be grasped with geometrical forms? Just as we must leave the region of commensurable numbers, it may well be that we must leave the region where reality can still be clothed in geometrical (or again arithmetical, algebraic, analytical) forms, such as in drawings of spirals and other figures derived from Geometry. So, in Geometry too, we should be coming into the incommensurable realm. In this sense it is indeed remarkable that in Embryology, though arithmetical analysis is not yet of much use, Geometry makes its presence felt pretty strongly the moment we begin to take hold of the embryological phenomena as they emerge from chaos. Here we are dealing, not indeed with incommensurable number but with something that tends to pass from incommensurable into commensurable form.
We have thus sought to grasp reality at two poles: On the one hand where the process of cognition leads through analysis into the incommensurable, and on the other where observation leads out of chaos to a grasping of reality in ever more commensurable forms. It is essential that we bring these things before our minds with full clarity, if we would add reality to what is presented by the external science of today. In no other way can we reach this end.
I should now like to add a methodical reflection, from which we can tomorrow make our way into more realistic problems.
In all that we have spoken of hitherto, we have been taking it for granted that the cosmic phenomena have been approached from the standpoint of Mathematics. It appeared that at one point the mathematician comes up to a limit—a limit he encounters too in purely formal Mathematics. Now there is something underlying our whole way of thinking in this realm, which perhaps passes unnoticed because it always wears the mask of the ‘obvious’ and we therefore never really face the problem. I mean the whole question of the application of mathematics to reality. How do we proceed? We develop Mathematics as a formal science and it appears to us absolutely cogent in its conclusions; then we apply it to reality, without giving a thought to the fact that we are really doing so on the basis of certain hypotheses. Today however, sufficient ground has already been created for us to see that Mathematics is only applicable to outer reality on the basis of certain premises. This becomes clear when we try to continue Mathematics beyond certain limits. First, certain laws are developed,—laws which are not obtained from external facts, as for example are Kepler's Laws, but from the mathematical process itself. They are in fact inductive laws, developed within Mathematics. They are then employed deductively; highly elaborate mathematical theories are built upon them.
Such laws are those encountered by anyone who studies Mathematics. In lectures given recently in Dornach by our friend Dr. Blumel, significant indications were given of this line of mathematical research. One of the laws in question is termed the Commutative Law. It can be expressed in saying: It is obvious that \(a+b\) equals \(b+a\), or \(a•b\) equals \(b•a\). This is a self-evident fact so long as one remains within the realm of real numbers: But it is merely an inductive law derived from the use of the implicit postulates in the arithmetic of real numbers.
The second law is the Associative Law. It is expressed as \((a + b) + c = a + (b + c)\). Again this is a law, simply derived by working with the implicit postulates in the arithmetic of real numbers.
The third is the so-called Distributive Law, expressible in the form: \(a (b + c) = ab + ac\). Once more, it is a law obtained inductively by working with the implicit postulates in the arithmetic of real numbers.
The fourth law may be expressed as follows: ‘A product can only equal zero if at least one of the factors equals zero.’ This law again is only an inductive one, derived by working with the implicit postulates in the arithmetic of real numbers.
We have, then, these four laws; the commutative law, the associative law, the distributive law, and this law about the product being equal to zero. These laws underlie the formal Mathematics of today, and are used as a basis for further work. The results are most interesting, there is no question of that. But the point is this: These laws hold good so long as we remain in the sphere of real numbers and their postulates. But no thought is ever given to the question, to what extent the real facts are in accord with them. Within our ordinary formal modes of experience it is true, no doubt that \(a + b = b + a\), but does it also hold good in outer reality? There is no ascertainable reason why it should. We might be very astonished one day to find that it did not work if we applied to some real process the idea that \(a + b\) equals \(b + a\). But there is another side to it. We have within us a very strong inclination to cling to these laws; with them therefore. We approach reality and everything that does not fit in escapes our observation. That is the other side.
In other words: We first set up postulates which we then apply to reality and take them as axioms of the reality itself. We ought only to say: I will consider a certain sphere of reality and see how far I get with the statement \(a + b = b + a\). More than that, I have no right to say. For by approaching reality with this statement we meet what answers to it, and elbow aside anything that does not. We have this habit too in other fields. We say for example, in elementary physics: Bodies are subject to the law of inertia. We define ‘inertia’ as consisting in the fact that bodies do not leave their position or alter their state of motion without a definite impelling force. But that is not an axiom; it is a postulate. I ought only so say: I will call a body which does not alter its own state of motion ‘inert’, and now I will seek in the real world for whatever answers to this postulate.
In that I form certain concepts, I am therefore only forming guiding lines with which to penetrate reality, and I must keep the way open in my mind for penetrating other facts with other concepts. Therefore I only regard the four basic laws of number in the right way if I see them as something which gives me a certain direction, something which helps me regulate my approach to reality. I shall [be] wrong if I take Mathematics as constituting reality, for then in certain fields, reality will simply contradict me. Such a contradiction is the one I spoke of, where incommensurability enters in, in the study of celestial phenomena.

