The Origins of Natural Science
GA 326
Lecture III
26 December 1922, Dornach
In the last two lectures I tried to indicate the point in time when the scientific outlook and manner of thinking, such as we know it today, arose in the course of time. It was pointed out yesterday that the whole character of this scientific thinking, emerging at the beginning most clearly in Copernicus’ conception of astronomy, depends on the way in which mathematical thinking was gradually related to the reality of the external world. The development of science in modern times has been greatly affected by a change—one might almost say a revolutionary change—in human perception in regard to mathematical thinking itself. We are much inclined nowadays to ascribe permanent and absolute validity to our own manner of thinking.
Nobody notices how much matters have changed. We take a certain position today in regard to mathematics and to the relationship of mathematics to reality. We assume that this is the way it has to be and that this is the correct relationship. There are debates about it from time to time, but within certain limits this is regarded as the true relationship. We forget that in a none too distant past mankind felt differently concerning mathematics. We need only recall what happened soon after the point in time that I characterized as the most important in modern spiritual life, the point when Nicholas Cusanus presented his dissertation to the world. Shortly after this, not only did Copernicus try to explain the movements of the solar system with mathematically oriented thinking of the kind to which we are accustomed today, but philosophers such as Descartes and Spinoza24Spinoza, Benedictus: Amsterdam 1632–1677. The Hague. Philosopher, mathematician, had Humanistic and Talmudistic training. By vocation, optician and politician. His main work Ethics with the characteristic full title Ethica Ordine Geometrica Demonstrata (Ethic Represented by Geometric Method) could only be published by his friends after his death. See Mysticism at the Dawn of the Modern Age and Riddles of Philosophy. began to apply this mathematical thought to the whole physical and spiritual universe.
Even in such a book as his Ethics, the philosopher Spinoza placed great value on presenting his philosophical principles and postulates, if not in mathematical formulae—for actual calculations play no special part—yet in such a manner that the whole form of drawing conclusions, of deducing the later rules from earlier ones, is based on the mathematical pattern. By and by it appeared self-evident to the men of that time that in mathematics they had the right model for the attainment of inward certainty. Hence they felt that if they could express the world in thoughts arranged in the same clear-cut architectural order as in a mathematical or geometrical system, they would thereby achieve something that would have to correspond to reality. If the character of scientific thinking is to be correctly understood, it must be through the special way in which man relates to mathematics and mathematics relates to reality. Mathematics had gradually become what I would term a self-sufficient inward capacity for thinking. What do I mean by that?
The mathematics existing in the age of Descartes25René Descartes: Lat., Renatus Cartenius, Le Haye (Tourraine) 1598–1650 Stockholm. Mathematician, physicist, philosopher. Educated by the Jesuits in La Fleche, he first became a soldier and was part of some campaigns but turned away from outer life to enter into the loneliness of a striver for knowledge, living first in Paris and then for a long time in Holland. He died in Stockholm, having been called there by Queen Christine. For him, doubt of tradition, but also of all sense perception, was the starting point of his philosophy and he found in self-consciousness the security of all being (“Cogito ergo Sum”). He developed the method of analytical geometry and gave an explanation of the rainbow. Main works: Essays, 1637, in it “Discours de la Methode and Dioptiric,” “Meditationes de Prima Philosophia,” 1641; “Passions de L'Ame,” 1650. See Riddles of Philosophy. and Copernicus can certainly be described more or less in the same terms as apply today. Take a modern mathematician, for example, who teaches geometry, and who uses his analytical formulas and geometrical concepts in order to comprehend some physical process. As a geometrician, this mathematician starts from the concepts of Euclidean geometry, the three-dimensional space (or merely dimensional space, if he thinks of non-Euclidean geometry.)26Non-Euclidian geometry is a prime example of “the self-contained inner ability to think.” C. Friedrich Gauss (1777–1855) discovered first that one can think more than only a geometric system. Because nobody understood this, he decided not to publish his results and to withdraw from the fruitless quarrel. Independently of Gauss in 1828 N.I. Lobatschewskij and in 1829 J. Boljai first published their solutions to the same problem. Rudolf Steiner often spoke about the meaning of this achievement, as in Wege und Ziele des geistigen Menschen in the lecture “Der Heutige Stand der Philosophie und Wissenschaft,” (Dornach, Switzerland: Rudolf Steiner Verlag, 1973; GA Bibl. Nr. 125). See also: Georg Unger, Physic am Scheidewege (Dornach: 1948), pages 19–28, and Vom Bielden Physikalischer Begriffe, Vol. 3 (Stuttgart: 1967), pages 31–32 and 193–194. In three-dimensional space he distinguishes three mutually perpendicular directions that are otherwise identical. Space, I would say, is a self-sufficient form that is simply placed before one's consciousness in the manner described above without questions being raised such as: Where does this form come from? Or, Where do we get our whole geometrical system?
In view of the increasing superficiality of psychological thinking, it was only natural that man could no longer penetrate to those inner depths of soul where geometrical thought has its base. Man takes his ordinary consciousness for granted and fills this consciousness with mathematics that has been thought-out but not experienced. As an example of what is thought-out but not experienced, let us consider the three perpendicular dimensions of Euclidean space. Man would have never thought of these if he had not experienced a threefold orientation within himself. One orientation that man experiences in himself is from front to back. We need only recall how, from the external modern anatomical and physiological point of view, the intake and excretion of food, as well as other processes in the human organism, take place from front to back. The orientation of these specific processes differs from the one that prevails when, for example, I do something with my right arm and make a corresponding move with my left arm. Here, the processes are oriented left and right. Finally, in regard to the last orientation, man grows into it during earthly life. In the beginning he crawls on all fours and only gradually, stands upright, so that this last orientation flows within him from above downward and up from below.
As matters stand today, these three orientations in man are regarded very superficially. These processes—front to back, right to left or left to right, and above to below—are not inwardly experienced so much as viewed from outside. If it were possible to go back into earlier ages with true psychological insight, one would perceive that these three orientations were inward experiences for the men of that time. Today our thoughts and feelings are still halfway acknowledged as inward experiences, but he man of a bygone age had a real inner experience, for example, of the front-to-back orientation. He had not yet lost awareness of the decrease in intensity of taste sensations from front to back in the oral cavity. The qualitative experience that taste was strong on the tip of the tongue, then grew fainter and fainter as it receded from front to back, until it disappeared entirely, was once a real and concrete experience. The orientation from front to back was felt in such qualitative experiences. Our inner life is no longer as intense as it once was. Therefore, today, we no longer have experiences such as this. Likewise man today no longer has a vivid feeling for the alignment of his axis of vision in order to focus on a given point by shifting the right axis over the left. Nor does he have a full concrete awareness of what happens when, in the orientation of right-left, he relates his right arm and hand to the left arm and hand. Even less does he have a feeling that would enable him to say: The thought illuminates my head and, moving in the direction from above to below, it strikes into my heart. Such a feeling, such an experience, has been lost to man along with the loss of all inwardness of world experience. But it did once exist. Man did once experience the three perpendicular orientation of space within himself. And these three spatial orientations—right-left, front-back, and above-below—are the basis of the three-dimensional framework of space, which is only the abstraction of the immediate inner experience described above.
So what can we say when we look back at the geometry of earlier times? We can put it like this: It was obvious to a man in those ages that merely because of his being human the geometrical elements revealed themselves in his own life. By extending his own above-below, right-left, and front-back orientations, he grasped the world out of his own being.
Try to sense the tremendous difference between this mathematical feeling bound to human experience, and the bare, bleak mathematical space layout of analytical geometry, which establishes a point somewhere in abstract space, draws three coordinating axes at right angles to each other and thus isolates this thought-out space scheme from all living experience. But man has in fact torn this thought-out spatial diagram out of his own inner life. So, if we are to understand the origin of the later mathematical way of thinking that was taken over by science, if we are to correctly comprehend its self-sufficient presentation of structures, we must trace it back to the self-experienced mathematics of a bygone age. Mathematics in former times was something completely different. What was once present in a sort of dream-like experience of three-dimensionality and then became abstracted, exists today completely in the unconscious. As a matter of fact, man even now produced mathematics from his own three-dimensionality. But the way in which he derives this outline of space from his experiences of inward orientation is completely unconscious. None of this rises into consciousness except the finished spatial diagram. The same is true of all completed mathematical structures. They have all been severed from their roots. I chose the example of the space scheme, but I could just as well mention any other mathematical category taken from algebra or arithmetic. They are nothing but schemata drawn from immediate human experience and raised into abstraction.
Going back a few centuries, perhaps to the fourteenth century, and observing how people conceived of things mathematical, we find that in regard to numbers they still had an echo of inward feelings. In an age in which numbers had already become an abstract ads they are today, people would have been unable to find the names for numbers. The words designating numbers are often wonderfully characteristic. Just think of the word “two.” (zwei) It clearly expresses a real process, as when we say entzweien, “to cleave in twain.” Even more, it is related to zweifeln, “to doubt.” It is not mere imitation of an external process when the number two, zwei, is described by the word Entzweien, which indicates the disuniting, the splitting, of something formerly a whole. It is in fact something that is inwardly experienced and only then made into a scheme. It is brought up from within, just as the abstract three-dimensional space-scheme is drawn up from inside the mind.
We arrive back at an age of rich spiritual vitality that still existed in the first centuries of Christianity, as can be demonstrated by the fact that mathematics, mathesis, and mysticism were considered to be almost one and the same. Mysticism, mathesis, and mathematics are one, though only in a certain connection. For a mystic of the first Christian centuries, mysticism was something that one experienced more inwardly in the soul. Mathematics was the mysticism that one experienced more outwardly with the body; for example, geometry with the body's orientations to front-and-back, right-and-left, and up-and-down. One could say that actual mysticism was soul mysticism and that mathematics, mathesis, was mysticism of the corporeality. Hence, proper mysticism was inwardly experienced in what is generally understood by this term; whereas mathesis, the other mysticism, as experienced by means of an inner experience of the body, as yet not lost.
As a matter of fact, in regard to mathematics and the mathematical method Descartes and Spinoza still had completely different feelings from what we have today. Immerse yourself in these thinkers, not superficially as in the practice today when one always wants to discover in the thinkers of old the modern concepts that have been drilled into our heads, but unselfishly, putting yourself mentally in their place. You will find that even Spinoza still retained something of a mystical attitude toward the mathematical method.
The philosophy of Spinoza differs from mysticism only in one respect. A mystic like Meister Eckhart or Johannes Tauler27Johannes Tauler: About 1300–1361 Strasbourg. Preacher and pastor, Dominican, mystic, student of Meister Eckhart. Sermons and writings in German by W. Lehmann, 1923; see also Mysticism at the Dawn of the Modern Age, the chapter “Friendship with God.” attempts to experience the cosmic secrets more in the depths of feeling. Equally inwardly, Spinoza constructs the mysteries of the universe along mathematical, methodical lines, not specifically geometrical lines, but lines experienced mentally by mathematical methods. In regard to soul configuration and mood, there is no basic difference between the experience of Meister Eckhart's mystical method and Spinoza's mathematical one. Anyone how makes such a distinction does not really understand how Spinoza experienced his Ethics, for example, in a truly mathematical-mystical way. His philosophy still reflects the time when mathematics, mathesis, and mysticism were felt as one and the same experience in the soul.
Now, you will perhaps recall how, in my book The Case for Anthroposophy,28Rudolf Steiner, The Case for Anthroposophy (London: Rudolf Steiner Press, 1970). I tried to explain the human organization in a way corresponding to modern thinking. I divided the human organization—meaning the physical one—into the nerve-sense system, the rhythmic system, and the metabolic-limb system. I need not point out to you that I did not divide man into separate members placed side by side in space, although certain academic persons have accused29In a reply to two lectures, which Walter Johannes Stein and Eugen Kolisko gave to defend two articles on “Anthroposophy as Science” in the Goettingen newspaper, Hugo Fuchs, Professor of Anatomy, spoke sarcastically of a human being with head, breast, and belly system. (From a report of the newspaper Die Dreigliederung des Sozialen Organismus, August 1920, No. 5). me of such a caricature. I made it clear that these three systems interpenetrate each other. The nerve-sense system is called the “head system” because it is centered mainly in the head, but it spreads out into the whole body. The breathing and blood rhythms of the chest system naturally extend into the head organization, and so on. The division is functional, not local. An inward grasp of this threefold membering will give you true insight into the human being.
Let us now focus on this division for a certain purpose. To begin with, let us look at the third member of the human organization, that of digestion (metabolism) and the limbs. Concentrating on the most striking aspect of this member, we see that man accomplishes the activities of external life by connecting his limbs with his inner experiences. I have characterized some of these, particularly the inward orientation experience of the three directions of space. In his external movements, in finding his orientation in the world, man's limb system achieves inward orientation in the three directions. In walking, we place ourselves in a certain manner into the experience of above-below. In much that we do with our hands or arms, we bring ourselves into the orientation of right-and-left. To the extent that speech is a movement of the aeriform in man, we even fit ourselves into direction of front-and-back, back-and-front, when we speak. Hence, in moving about in the world, we place our inward orientation into the outer world.
Let us look at the true process, rather than the merely illusionary one, in a specific mathematical case. It is an illusionary process, taking place purely in abstract schemes of thought, when I find somewhere in the universe a process in space, and I approach it as an analytical mathematician in such a way that I draw or imagine the three coordinate axes of the usual spatial system and arrange this external process into Descartes’ purely artificial space scheme.

This is what occurs above, in the realm of thought schemes, through the nerve-sense system. One would not achieve a relationship to such a process in space if it were not for what one does with one's limbs, with one's whole body, if it were not for inserting oneself into the whole world in accordance with the inward orientation of above-below, right-left, and front-back. When I walk forward, I know that on one hand I place myself in the vertical direction in order to remain upright. I am also aware that in walking I adjust my direction to the back-to-front orientation, and when I swim and use my arms, I orient myself in right and left. I do not understand all this if I apply Descartes’ space scheme, the abstract scheme of the coordinate axes. What gives me the impression of reality in dealing with matters of space is found only when I say to myself: Up in the head, in the nerve system, an illusory image arises of something that occurs deep down in the subconscious. Here, where man cannot reach with his ordinary consciousness, something takes place between his limb system and the universe. The whole of mathematics, of geometry, is brought up out of our limb system of movement. We would not have geometry if we did not place ourselves into the world according to inward orientation. In truth, we geometrize when we lift what occurs in the subconscious into the illusory of the thought scheme. This is the reason why it appears so abstractly independent to us. But his is something that this only come about in recent times. In the age in which mathesis, mathematics, was still felt to be something close to mysticism, the mathematical relationship to all things was also viewed as something human.
Where is the human factor if I imagine an abstract point somewhere in space crossed by three perpendicular directions and then apply this scheme to a process perceived in actual space? It is completely divorced from man, something quite inhuman. This non-human element, which has appeared in recent times in mathematical thinking, was once human. But when was it human?
The actual date has already been indicated, but the inner aspect is still to be described. When was it human? It was human when man did not only experience in his movements and his inward orientation in space that he stepped forward from behind and moved in such a way that he was aware of his vertical as well as the horizontal direction, but when he also felt the blood's inward activity in all such moving about, in all such inner geometry. There is always blood activity when I move forward. Think of the blood activity present when, as an infant, I lifted myself up from the horizontal to an upright position! Behind man's movements, behind his experience of the world by virtue of movements, (which can also be, and at one time was, an inward experience) there stands the experience of the blood. Every movement, small or large, that I experience as I perform it contains its corresponding blood experience. Today blood is to us the red fluid that seeps out when we prick our skin. We can also convince ourselves intellectually of its existence. But in the age when mathematics, mathesis, was still connected with mysticism, when in a dreamy way the experience of movement was inwardly connected with that of blood, man was inwardly aware of the blood. It was one thing to follow the flow of blood through the lungs and quite another to follow it through the head. Man followed the flow of the blood in lifting his knee or his foot, and he inwardly felt and experienced himself through and through in his blood. The blood has one tinge when I raise my foot, another when I place it firmly on the ground. When I lounge around and doze lazily, the blood's nuance differs from the one it has when I let thoughts shoot through my head. The whole person can take on a different form when, in addition to the experience of movement, he has that of the blood. Try to picture vividly what I mean. Imagine that you are walking slowly, one step at a time; you begin to walk faster; you start to run, to turn yourself, to dance around. Suppose that you were doing all this, not with today's abstract consciousness, but with inward awareness: You would have a different blood experience at each stage, with the slow walking, then the increase in speed, the running, the turning, the dancing. A different nuance would be noted in each case. If you tried to draw this inner experience of movement, you would perhaps have to sketch it like this (white line.) But for each position in which you found yourself during this experience of movement, you would draw a corresponding inward blood experience (red, blue, yellow—see Figure 2)
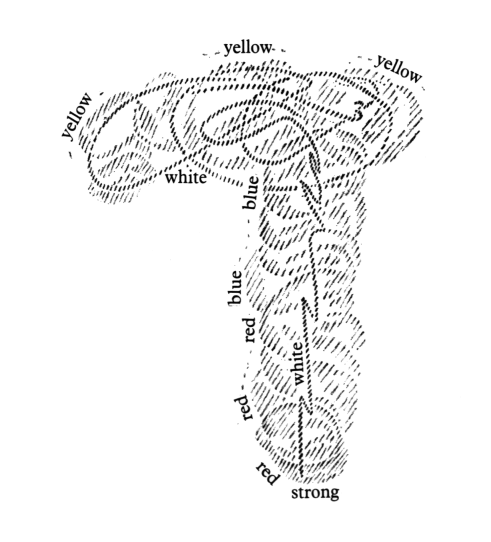
Of the first experience, that of movement, you would say that you have it in common with external space, because you are constantly changing your position. The second experience, which I have marked by means of the different colors, is a time experience, a sequence of inner intense experiences.
In fact, if you run in a triangle, you can have one inner experience of the blood. You will have a different one if you run in a square.
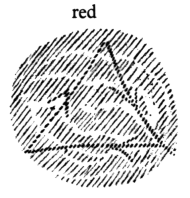
What is outwardly quantitative and geometric, is inwardly intensely qualitative in the experience of the blood.
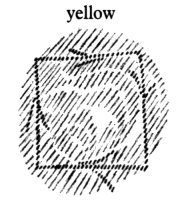
It is surprising, very surprising, to discover that ancient mathematics spoke quite differently about the triangle and the square. Modern nebulous mystics describe great mysteries, but there is no great mystery here. It is only what a person would have experienced inwardly in the blood when he walked the outline of a triangle or a square, not to mention the blood experience corresponding to the pentagram. In the blood the whole of geometry becomes qualitative inward experience. We arrive back at a time when one could truly say, as Mephistopheles does in Goethe's Faust, “Blood is a very special fluid.”30From Goethe's Faust, Part I, the scene in the Student Room with Faust and Mephisto. See Rudolf Steiner, The Occult Significance of the Blood (London: Rudolf Steiner Press, 1967). This is because, inwardly experienced, the blood absorbs all geometrical forms and makes of them intense inner experiences. Thereby man learns to know himself as well. He learns to know what it means to experience a triangle, a square, a pentagram; he becomes acquainted with the projection of geometry on the blood and its experiences. This was once mysticism. Not only was mathematics, mathesis, closely related to mysticism, it was in fact the external side of movement, of the limbs, while the inward side was the blood experience. For the mystic of bygone times all of mathematics transformed itself out of a sum of spatial formations into what is experienced in the blood, into an intensely mystical rhythmic inner experience.
We can say that once upon a time man possessed a knowledge that he experienced, that he was an integral part of; and that at the point in time that I have mentioned, he lost this oneness of self with the world, this participation in the cosmic mysteries. He tore mathematics loose from his inner being. No longer did he have the experience of movement; instead, he mathematically constructed the relationships of movement outside. He no longer had the blood experience; the blood and its rhythm became something quite foreign to him. Imagine what this implies: Man tears mathematics free from his body and it becomes something abstract. He loses his understanding of the blood experience. Mathematics no longer goes inward. Picture this as a soul mood that arose at a specific time. Earlier, the soul had a different mood than later. Formerly, it sought the connection between blood experience and experience of movement; later, it completely separated them. It no longer related the mathematical and geometrical experience to its own movement. It lost the blood experience. Think of this as real history, as something that occurs in the changing moods of evolution. Verily, a man who lived in the earlier age, when mathesis was still mysticism, put his whole soul into the universe. He measured the cosmos against himself. He lived in astronomy.
Modern man inserts his system of coordinates into the universe and keeps himself out of it. Earlier, man sensed a blood experience with each geometrical figure. Modern man feels no blood experience; he loses the relationship to his own heart, where the blood experiences are centered. Is it imaginable that in the seventh or eighth century, when the soul still felt movement as a mathematical experience and blood as a mystical experience, anybody would have founded a Copernican astronomy with a system of coordinates simply inserted into the universe and totally divorced from man? No, this became possible only when a specific soul constitution arose in evolution. And after that something else became possible as well. The inward blood awareness was lost. Now the time had come to discover the movements of the blood externally through physiology and anatomy. Hence you have this change in evolution: On one hand Copernican astronomy, on the other the discovery of the circulation of the blood by Harvey,31William Harvey, 1578–1658, physiologist, Professor of Anatomy, London, discoverer of the main bloodstream: De Motu Cordis et Sanguinis (1628). a contemporary of Bacon and Hobbes. A world view gained by abstract mathematics cannot produce anything like the ancient Ptolemaic theory, which was essentially bound up with man and the living mathematics he experienced within himself. Now, one experiences an abstract system of coordinates starting with an arbitrary zero point. No longer do we have the inward blood experience; instead, we discover the physical circulation of the blood with the heart in the center.
The birth of science thus placed itself into the whole context of evolution in both its conscious and unconscious processes. Only in this way, out of the truly human element, can one understand what actually happened, what had to happen in recent times for science—so self-evident today—to come into being in the first place. Only thus could it even occur to anybody to conduct such investigations as led, for example, to Harvey's discovery of the circulation of the blood. We shall continue with this tomorrow.

